Frank-Kasper相是指一大类最早在金属合金中发现的、具有复杂晶体结构的拓扑密堆相。人们近年来才在各种软物质体系中也发现了它们，这使得对它们在软物质体系中的形成机理和结构调控的研究成为了热点。特别是2010年在构象不对称的双嵌段共聚物熔体（以下简记为A-B）中发现的Frank-Kasper ó相，突破了人们此前对这种最简单的嵌段共聚物体系的自组装行为的认知。目前已经有多个实验团队在该体系中发现了稳定的ó和A15相，这也和一些课题组用“标准”模型所做的自洽场理论计算的结果定性吻合。
       作为一种平均场理论，自洽场理论忽略了体系的涨落和关联效应。对于A-B，这些效应的大小可以用与实验中的链长N成正比的等效聚合度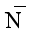来表征。自洽场理论对应于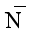→∞的极限情况，而所有在实验中形成Frank-Kasper相的A-B的N都比较小，对应于25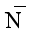＜＜385（只有一个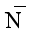≈520的例外；作为参考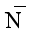：≈1000的接近于对称的聚苯乙烯-聚甲基丙烯酸甲酯（PS-PMMA）所形成的层状相周期约为23纳米），因此体系的涨落和关联效应对于这些低分子量的A-B应该有着不可忽略的影响。另一方面，目前所有用“标准”模型而得到的自洽场理论计算结果均高估了在实验中形成Frank-Kasper相所需的构象不对称性（由短嵌段A与长嵌段B的统计链段长度比值的平方å来表征）。通过将自洽场理论结果与基于同一模型的分子模拟结果进行对比，就可以明确、定量地揭示出前者所忽略的涨落和关联效应。但是，在自洽场理论计算中最常用的“标准”模型却无法直接用于分子模拟，这是因为该模型使用了连续高斯链（即每条链上有无穷多个链节）、在A和B链节之间采用了Dirac ä函数形式（即作用距离为0）的排斥作用势、以及在连续空间中运用了不可压缩条件（即A和B链节的数密度之和在每个空间点上都是一样的）。

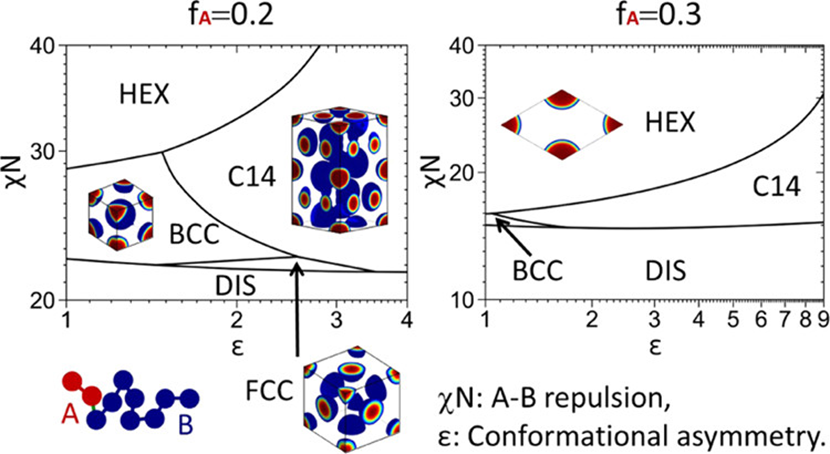
图1. 双嵌段共聚物熔体（A-B）的耗散粒子动力学模型的自洽场相图。
为了解决上述问题，美国科罗拉多州立大学化学与生物工程系王强教授的课题组针对构象不对称的A-B提出了一个耗散粒子动力学（DPD）模型，并通过高精度的、采用GPU大规模并行的自洽场理论计算构造了该模型在÷N-å空间中的相图（图1）。该DPD模型使用了离散高斯链（即每条链上有N=10个链节）、在所有链节之间都采用了作用距离大于0的DPD对势（即体系是可压缩的）、并在A和B链节之间还另加了由参数÷>0来调控的DPD对势。由于该模型可以直接用于DPD模拟，因此它的自洽场计算结果不需要通过任何参数拟合就能够直接地与它的DPD模拟结果进行对比，从而明确、定量地揭示出在自洽场理论中所忽略的涨落和关联效应的影响。而与“标准”模型相比，DPD模型的自洽场理论在计算有序相时所需要的时间和内存都至少要少一个数量级，因此在相同的计算能力下可以得到更精确的结果。
       该课题组研究了五种Frank-Kasper相（即 A15、C14、C15、Z和ó相）和四种常规相（即按照体心立方和面心立方排列的球状相、按照正六角排列的柱状相、以及无序相，分别记为BCC、FCC、HEX和DIS），并发现在他们计算的参数范围内C14是唯一稳定的Frank-Kasper相（图1）。他们的计算结果表明：(1) 类似于ó和A15相，C14的稳定性源于A-B的构象不对称（即å>1）；(2) C14在所有的有序相中具有最大的熵密度；(3) 在å>1时，DPD模型的自洽场相图与文献中“标准“模型的自洽场相图存在着很大的差别，而这些差别却不太可能是由这两个模型的不同引起的，于是这对以前用“标准”模型所做的Frank-Kasper相的自洽场理论计算的精度是否足够高提出了质疑。更详细的内容还请见原文及其补充材料。
       该项研究通过自洽场理论计算首次预测了由A-B形成的稳定的C14相。虽然这和一个实验团队最近在A-B中发现了稳定的C14相的结果定性吻合，后者却在其它条件下还得到了稳定的ó和A15相。鉴于实验体系和模型体系有着诸多的不同（例如体系的多分散性、÷值等等），该课题组下一步的工作是使用他们提出的DPD模型对构象不对称的A-B进行DPD模拟，并通过将它的模拟结果与上面的自洽场理论计算结果直接对比来明确、定量地揭示出体系的涨落和关联效应对Frank-Kasper相的结构和稳定性的影响。
       上面所介绍的工作以“Frank–Kasper Phases of Diblock Copolymer Melts Studied with the DPD Model: SCF Results”为题发表在《Macromolecules》上（Macromolecules 2022, 55 (19), 8931–8939; DOI: 10.1021/acs.macromol.2c00933）。文章的第一作者是美国科罗拉多州立大学化学与生物工程系的博士生何俊橦。该研究得到了美国能源部的支持。

原文链接：

https://doi.org/10.1021/acs.macromol.2c00933